Chapter 1
- Chapter Sections
- Section 1.1: Variables and Operators (problems)
- Section 1.2: Using Functions (problems)
- Section 1.3: Creating Functions (problems)
- Section 1.4: Python Files and Modules (problems)
- Section 1.5: If Statements (problems)
- Section 1.6: While Loops (problems)
Introduction
Although computers can be programmed to run countless types of software - everything from games, to word processors, to weather simulations - at its heart a computer is a powerful calculating machine. In many ways a computer is an extremely powerful calculator with some extra features. Because of this Computer Science is a subject that has close connections to math. Computer code itself can often look a lot like math. For example, like in a math class, there are variables that could be set to different numbers and operators like addition, subtraction, multiplication, and division. However, we will see later that the programming tools that have been developed will enable us to create software with no obvious links to a calculating machine.
In this first chapter we explore the more direct links to mathematics. In the first section the basics of defining variables and using operators such as addition and multiplication are discussed. The next two sections concern defining functions which in many ways resemble mathematical functions. In the last two section conditional statements are discussed that will enable us to, for example, work with inequalities and count.
Section 1.1: Variables and Operators
Defining Variables
Like a math class, we can define variables that store numbers. Unlike a math class, we can define variables that store text and other data types. In computer science, a piece of text is called a string because it is a string or sequence of characters (letters, numbers, etc.).
Python Code Sample
x = 102 @
y = -30 @
name = "Fred" @
greeting = "Hello, my name is Fred." @
var = "123"
The Python code above creates 4 variables. The gray numbers on the side are the line numbers and are not part of the code. Quotes are used to let Python know you are creating a string. Without the quotes, any number is just a number and any word is assumed to not be a string, like a variable. When there are quotes around a number, then the variable stores a string containing those digits, not an actual number. This will be discussed in greater detail in later chapters. The quotes themselves are not part of the string, they just denote that it is a string and not a variable. Note also that the lines of code are executed in the order that they appear, so x is defined first and so on...
Operators
An operator is just a symbol (sometimes technically two symbols) that does something, usually basic and important.
Some Common Operators
| Code | Name | Description |
| + | Addition | Adds two numbers or other data types. |
| - | Subtraction | Subtracts two numbers or other data types. |
| * | Multiplication | Multiples two numbers or other data types. |
| ** | Exponentiation | Raises the first number to the power of the second number. |
| / | Division | Divides two numbers or other data types. |
| = | Assignment |
Creates a new variable with a new value or changes an existing variable to a new value.
Assignment is always to the left. |
| += | Increment | Adds to an existing variable by an amount. The variable is always on the left and the amount added is always on the right. |
| -= | Decrement |
Subtracts from an existing variable by an amount. |
Python Code Sample
x = 11 @
y = 9 @
z = x - y @
z += 3
What is stored in the variable z after these lines of code are done executing? If you answered 5 then you are correct. In the lines of code above, first x is set equal to 11, then y to 9. Then z is set equal to the difference of x and y, which is 2. But then the line of code z += 3 takes the existing value of z, which is 2, and adds 3.
Creating Variables VS. Modifying Variables
There is a very important, but subtle, distinction between the = operator and the += operator. In Python, the = operator has the power to create a new variable. The += and -= operators can only modify a variable. The = operator is not always used to create a new variable, it can also be used to modify an existing variable by reassigning a value to it.
The
= operator vs. the
+= operator:
| Code | Description |
| x = 100 | Creates a new variable called x. |
| x += 20 | Modifies the variable x. |
| y = 0 | Creates a new variable called y. |
| y = 10 | Modifies the variable y by changing its value. |
| s = "A String" | Creates a new string variable called s. |
Errors
There are, unfortunately, may ways of creating errors when programing. Python will
give you error messages when something goes wrong.
Common Errors
- Trying to modify or use a variable that does not exist.
- Incorrectly using an operator. Operator are not always symmetrical. For example, the left side of an assignment operator is changed so that it equals the right side.
- Trying to change a literal, which is a specific number or other type that appears in the code.
Error?
| Code | Error? |
| x = 100 | This is fine. A new variable is created. |
| y += 10 | ERROR. The variable y has not been created. |
| x -= 20 | This is fine. The variable x already exists so it is okay to modify it. |
| z = x + 3 | This is fine. A new variable called z is created and x already exists. |
| a = 2 | This is fine. |
| c = a + b | ERROR. Although there is a variable a, there is no variable b. |
| 5 = a | ERROR. We cannot change the number 5 to be the same as 2. 5 is a literal, not a variable. |
| s = "potato" | This is fine. |
Variable Name Rules
The names we use for variables or other identifiers follow certain rules. If the rules are violated then there will be errors.
- Variable names cannot have blank spaces. Use an underscore instead.
| fish_stick | This is okay because it has an underscore. |
| fish stick | This will most likely create an error. Python will think you mean two variables. |
- Variable names can be as long as you want, but if they are too long your code will be hard to read and understand.
- Variable names must start with a letter or underscore.
- Numbers can be part of a variable name, but numbers cannot start the variable name.
- Other symbols are not allowed, such as $, %, #,...
| var2 | This is okay. |
| 2ndvar | This will create an error. |
| _var | This is okay. |
| the_2nd_var | This is okay. |
| k$s | This will create an error. |
- Variable names are CAsE SeNsITIve. The variable names var, Var, VAR, and vaR look like different variables to Python.
Section 1.1 Name:____________________
Variables and Operators
Score: /5
Problems
- Vocabulary Matching: Match each term with the best fitting description.
| string | ___ A constant value. |
| operator | ___ Can be set to different values. |
| variable | ___ Text data. |
| literal | ___ Performs a simple, but important, task. |
- What will be stored in the variable x after the following lines of code:
x = 50
x += 10
|
y = 10
z = 25
x = y + z
|
y = 5
x = 3 * y
x -= 10
|
a = 2 ** 3
x = a / 4
x += a
|
m = 10
x = 5
x = x + m
|
x = 2
x = x*x
x = x*x
|
- Which lines of code would create an error? Cross out any lines that create an error and assume that line will not affect later lines.
var = 22 @
VAR += 10 @
var2 += 10 @
var3 = "Fish" @
aaa = var + 10 @
67 = var @
55 -= 10 @
n = a + b @
yasjd = 4
- Circle all variable names that are acceptable in Python.
- num
- num2
- 3num
- a_num
- 4_num
- large num
- small_num
- _num_
- num_2
- money$
- no!_way
Section 1.2: Functions
Functions
Another connection between math and computer science is the topic of functions. Like in a math class, a function can take a value and return a value. Unlike a mathematical function, functions in programming languages like Python do not always take a value or return a value.
The mathematical notation for a function looks like f(x)=5x+3. This is a math function that takes a number called x and multiplies it by 5, then adds 3. This notation is a way to say what the function does.
Math Function Notation (not computer code):
f(x) = 5x+3 @
f(1) = 5(1)+3 = 8 @
f(2) = 5(2)+3 = 13 @
f(-1) = 5(-1)+3 = -2
Note: The parenthesis after the letter f does not mean multiplication. The parenthesis are a way of saying that we are putting this number into the function f. This function turns the number 1 into the number 8, 2 into 13 and so on...
Functions in Programming Languages
The Python programming language comes with a large number of math functions. To access these math functions we need to open a file called math. In Python, a file containing already created code is called a module. Python comes with the math module already created for us to use. We can also create our own modules, more on this in the next section. To use the math module we need a line of code: from math import *.
You will likely notice as you begin to program that certain important words (called keywords) will usually change color to make the words easier to identify. The colors scheme used depends on the program being used to write the code. The keyword import tells Python to find the module so that it can be used.
Using the sqrt (Square Root) function in the math module:
from math import * @
a = sqrt(4) @
b = sqrt(9) @
c = sqrt(16)
After these lines of code execute, the variables a, b, c will store the numbers 2, 3, 4. The math function sqrt takes the number given to it and finds the square root of that number. Other math functions include: log, sin, cos, tan.
Notice that the way the code is written for a programming function looks very similar to math notation. The word syntax refers to the way something is written in code, including which symbols are used and the arrangement of the symbols. With Python's syntax, the result is stored on the left. In the example above, the variables a, b and c store the results of the function. This syntax is a little different than typical mathematical notation where the result is often written on the right.
Another useful built-n Python function is called randint and it is contained in the module random. This function generates random integers. Unlike the sqrt function, the randint function takes two numbers, the minimum and the maximum. The numbers that are created are unpredictable to the user and also the programmer.
Using the randint function in the random module:
from random import * @
x = randint(1,10) @
y = randint(1,100) @
z = randint(-100,100)
- After these lines of code execute, the variables x, y, z will store integers in the ranges provided. For example, the variable x will store one of the following numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. But, we cannot predict which one.
- Negative integers are acceptable for both the minimum and the maximum, but the minimum needs to always be smaller than the maximum.
- The minimum is always the first number, the maximum is always the second.
Composition of Functions
One math topic that students in Algebra classes often find confusing is the composition of functions. When we compose functions we take the answer of one function and put that number into the next function. With programming, we can also compose functions, which often reduces the amount of code we need to write. With both math and programming, when we have two functions, lets say f(x) and g(x), we can take the value of one function and put that into the other function: f(g(x)).
Composition of Math Functions:
f(x) = 2x-3 @
g(x) = 3x+1 @@
f(g(2)) = f(7) = 11 @
g(f(2)) = g(1) = 4 @
f(g(f(1))) = f(g(-1)) = f(-2) = -7
Chains of functions that are composed together can be as long as we want them to be.
Composition of Programming Functions:
from math import * @
from random import * @@
x = randint(sqrt(4), 10) @
y = randint(7, sqrt(100)) @
z = randint( sqrt(16), sqrt(81) )
The sqrt function is evaluated first because it is inside of the randint function in the examples above. The variable x is in the range 2, 3, 4, 5, 6, 7, 8, 9, 10, while z is in the range 4, 5, 6, 7, 8, 9.
Section 1.2 Name:____________________
Functions
Score: /5
Problems
- Vocabulary Matching: Match each term with the best fitting description.
| syntax | _____ An example of a programming function that returns the square root of a number. |
| composition | _____ The way code should be written for a particular programming language. |
| sqrt | _____ Combining several functions in a certain order. |
| randint | _____ A type of function that always takes a value and returns a value. |
| mathematical function | _____ A type of function that may or may not take a value and may or may not return a value. |
| programming function | _____ An example of a programming function that returns random numbers. |
- Math Function Review: Using the math function f(x) = 3x - 7, find what the following variables are equal to?
- y = f(10), what is y equal to?
- n = f(-3), what is n equal to?
- g = f(2), what is g equal to?
- More Math Function Review: For the following math functions, f(x) = 2x+1, g(x) = 3x-2, h(x) = x+2 find what the following variables are equal to?
- q = f(g(1)), what is q equal to?
- n = g(h(2)), what is n equal to?
- t = h(f(-1)), what is t equal to?
- m = h(g(f(0))), what is m equal to?
- w = f(g(h(f(-1)))), what is w equal to?
- What are the possible values of the following programming variables?
- q = randint(1,8), what could q be equal to?
- n = randint(-5,0), what could n be equal to?
- t = randint( sqrt(16), sqrt(36) ), what could t be equal to?
- g = randint( sqrt(9), 10 ), what could g be equal to?
- Write Code: Complete the following code to perform the following tasks.
- Write code that will store the square root of 700 in a variable.
from math import * @@@
- Write code that will store a random integer between -1000 and 1000 in a variable.
from random import * @@@
Section 1.3: Creating Functions
Defining New Functions
Like variables, it is possible with Python and other programming languages to define (create) your own functions However, defining your own functions is more complicated than defining variables.
The keyword def is used to tell the Python interpreter that we are defining a new function. We also must indent the code that follows if it is part of the function. Often will need to return an answer. To do this we need to use the keyword return.
A Simple Function
def f(x): @
~y = x*x @
~return y
A function always starts with the def keyword. We know the line 2 and 3 are part of the function because they are intended. Question: What math function is this equivalent to?
Using A Function
def f(x): @
~return x*x @@
a = f(2) @
b = f(3) @
c = f(4)
Notice that the lines containing the variables a, b, and c are not indented. These lines are not part of the function, but instead use the function. Once the function has been defined, it can be used over and over again. Notice also that line 3 is blank. This makes the code easier to read, but it is not necessary. What do you think will be stored in the variables a, b, and c?
Defining multiple functions.
def f(x): @
~return 5*x+3 @@
def g(a, b): @
~return a + b - 100 @@
def some_function(t): @
~return 100*t
We know in the code above which lines of code are contained in which functions because those lines are indented and follow the name of the function. Also, note that in this example we have composed the math formulas with the return keyword to simplify the code inside the functions.
Programming Functions Are Not Always Like Math Functions
- A function you create does not need to have any arguments.
- A function you create does not need to return anything. In other words, there does not need to be an answer. A programming function of this type executes collection of lines of code that may do several things, but there is no single resulting number or other type.
Blueprint of a Function
The basic parts of a function include the function header and body. The header contains the def keyword and the name of the function, followed by any arguments that the function requires. Arguments are variables for things that come from outside the function that the function requires to work correctly. At the very end of the header there is always a colon ":". Do not forget to type the ":". The body includes all of the remaining code that the function executes when it is used. All of the lines of code inside the body of the function must be indented. If the function returns a value, then the last line of code in the body must use the return keyword.
Function Blueprint
def function_name(argument_1, argument_2,... ): @
~body @
~return answer
It is possible to create functions in Python with no arguments, or functions with as many as 256 arguments. However, functions with too many arguments are difficult to use. A good rule of thumb is to limit the number of function arguments to 3 or 4. Below is a simple example of a function with no arguments.
A Function With No Arguments
def simple_function(): @
~return("This function does not do much")
Note that the parenthesis, (), are still required even if there is no argument between them. The parenthesis are the primary way we know we are dealing with a function and not a variable.
Blocks and Headers
Function bodies are one example of what are called blocks. We will see in the next few sections other types of blocks. In all cases blocks are indented and have headers. A header, whether or not it is a function header, always ends with a colon : . The lines that make up a block of code, such as a function body, are always executed together.
A Few Functions
def f(x): @
~y = x*x @
~return y @@
def g(x): @
~return 1/x @@
def h(x): @
~y = x*x @
~y += 1/x @
~return y
In the example above, the lines 2 and 3 form a single block. The header of this block is at line 1. Likewise, the lines 6 forms a one line block whose header is at line 5. What is the remaining block and what is its header?
Local Variables
Variables that are created inside of a function are called local variables. Local variables do not exist outside of the function. Trying to use a local variable outside of a function will create an error.
Local Variables
def func(a): @
~b = a*a*a @
~return b @ @
y = func(2) @
z = b ~<--- ERROR
In this example, the variables y and z are defined outside of the function. The variable b is inside of the function and, therefore, a local variable. Trying to use b outside of the function will create an error.
A Function With Two Arguments
def f(a, b): @
~return a-b @ @
a = 10 @
b = 7 @
c = f(b,a)
In this example, one might assume that c is equal to 3. However, this would be wrong. Since on line 6 the external variable b is put in the first argument position, the value stored in the external variable b is copied to the local variable a. Likewise the value of external variable a is copied to the local variable b. So the variable c is equal to f(10,7) which is -3.
Section 1.3 Name:____________________
Creating Functions
Score: /5
Problems
- Vocabulary Matching: Match each term with the best fitting description.
| Function Header | _____ The part of a function that contains the lines of code that the function executes when it is used. |
| Function Body | _____ A variable that is defined inside of a function and only works inside of the functions. |
| Function Argument | _____ A keyword used at the end of a function, if it is used at all. |
| Local Variable | _____ A keyword used to let Python know that a new function is being created. |
| def | _____ The part of a function that contains the def keyword and the name of the function. |
| return | _____ A variable containing data from outside of the function. |
- Which lines of code would create an error? Cross out any lines that would create an error and assume that line will not affect later lines.
m = 101 @
def func(q, w): @
~x = q*w @
~return x @@
m += func(2,3) @
n = x + 100 @
g = func(1,4) + 823
- Which lines of code would create an error? Cross out any lines that would create an error and assume that line will not affect later lines.
def func(a, b): @
~y = 2*a-3*b @
~y += 10 @
~return y @@
p += func(2,3) @
n = y + 100 @
x = func(a,b) + 823
- For each part, find y.
A function
def fn(a, b, c): @
~return 2*a + b - c
Part (a)
y = fn(2,3,5)
Part (b)
n = 4 @
y = fn(3,n,2)
Part (c)
n = 1 @
a = 7 @
y = fn(n,a,1)
Part (d)
a = 4 @
b = 2 @
c = 5 @
y = fn(c,a,b)
- For the following functions,
def func_one(x): @
~return 1/x @@
def func_two(x): @
~y = x*x @
~return y @@
def func_three(x): @
~y = x*x @
~y += 1/x @
~y += 30 @
~return y
- Which function is line 6 a part of?
- Which function is line 11 a part of?
- Which function is line 9 a part of?
- Write Some Code:
- Write code for a function that multiplies two numbers and returns the answer.
@@@@
- Write code for a function that find the average of two numbers and returns the answer.
@@@@
Section 1.4: Python Files and Modules
Introduction
Any variables or functions you have created can be saved to a file called a Python file. The extension for a Python file is '.py'. In addition to saving your work, it is also possible to link different files together so that code in one file can be used in another file. Python files are sometimes called modules. There are also many built-in modules or modules that can be installed with many useful features.
The import Keyword
The keyword import tells Python where to look up variable names and other things defined in a module. Although there are several ways to write code to import a file, we will use one method in particular. Note, the '.py' extension is not included in the code even when the file has this extension.
Line of Code that will import a file:
- from file_name import *
In the code above the asterick, *, can be thought of as meaning everything. The line of code above imports everything from a file called file_name.py
Import Hierarchies
For large and complex programs it is common to import modules that, in turn, import other modules. Frequently, the modules will be arranged in a hierarchy, each module may import other modules that are needed to function. Below is an example of a module hierarchy used by a complex program.
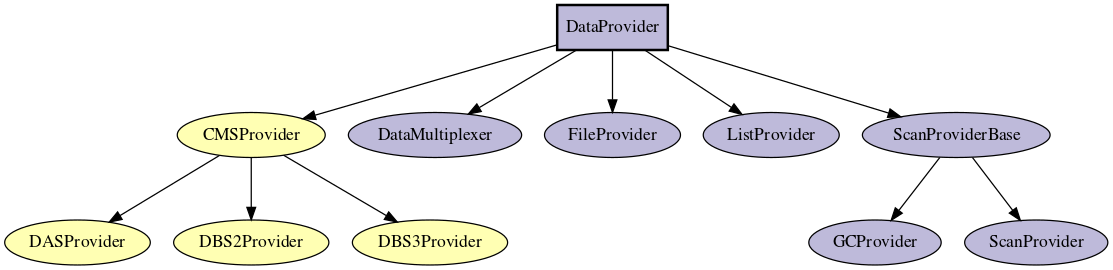
Very Simple Module Hierarchy
File: mod1.py
x = 10
File: mod2.py
from mod1 import * @
y = 5 + x
File: mod3.py
from mod2 import * @
z = x + y
Section 1.4 Name:____________________
Python Files and Modules
Score: /5
Problems
- Vocabulary Matching: Match each term with the best fitting description.
| module | _____ A keyword that tells Python which modules to use. |
| import | _____A Python File that stores general and useful code. |
- For the following file, write another module that multiplies the variables var1 and var2 and stores the result in a variable var3.
var_file.py
var1 = 7 @
var2 = 4
@@@@
- For the following file, write another module that subtracts the variables big_var and small_var and stores the result in a variable sub.
var_file.py
big_var = 77 @
small_var = 33
@@@@
- For the following file, write another module that adds the variables a, b and c and stores the result in a variable d.
abc_file.py
a = 30 @
b = 100 @
c = 50
@@@@
Section 1.5: If-Statements
Introduction
There are times when we need to execute code when certain conditions are met. For example, if we are assigning letter grades based on the score of a test, we will likely need to check if the score was within the range for an A, or a B and so on, then assign accordingly.
In order to make some lines of code depend on a condition, we need a few new Python keywords. Python has 3 keywords for working with conditions: if, else and elif. The keywords if and else are fairly intuitive. The keyword elif stands for "else if" and is a combination of the other two.
Simplest If-Structure
if condition: @
~do something
The word condition represents a statement, such as an inequality, that is either true or false. If the condition is false, then the lines of code after the if are skipped over and are not executed. Note the lines of code following the if keyword must be indented. These lines form a block of code that are executed together. The header of the block is the if keyword, followed by the condition, followed by : . Any lines of code that are not indented are not part of the block and are not dependent on the condition. This is very similar to functions where we used indentation to determine the block that made up the function body. Just like with functions, do not forget to write : at the end of the header or you will get an error message and the code will not work.
if score > 89: @
~grade = "A"
What if score = 88?
In the above example, the variable grade is not assigned to be "A" because the condition is false. The variable grade in this example is not initialized at all and we would get an error if we tried to used it in a later section of code.
If-Structure with else
if condition: @
~do something @
else: @
~do some other thing
The else keyword is used to execute alternative lines of code. If the condition is false, the lines of code after else will run instead. If the condition is true, then the lines of code after else will be skipped. Like with if, the lines of code after else must be indented.
if score > 89: @
~grade = "A" @
else: @
~grade = "F"
What if score = 94?
What if score = 88?
In the above example, the variable grade is assigned to "F" as an alternative to being assigned to "A". A somewhat harsh grade for an 88. The elif keyword will allow us to create a wider range of possibilities.
If-Structure with elif and else
if condition: @
~do something @
elif second_condition: @
~do something different @
else: @
~all conditions are false so do this instead
The elif keyword is used to execute alternative lines of code that are dependent on another condition. Note the second condition is not checked at all unless the first condition is false. With if, else and elif it is possible to create chains of conditions that are checked one after another until a condition is found to be true or the else keyword is reached. As soon as a true condition is found, the corresponding block is executed and the chain stops.
if score > 89: @
~grade = "A" @
elif score > 79: @
~grade = "B" @
elif score > 69: @
~grade = "C" @
elif score > 59: @
~grade = "D" @
else: @
~grade = "F"
What if score = 62?
What if score = 103?
What if score = -7?
Now, the variable grade is assigned to the much more reasonable grade of "B". It is important to note that there is no limit to how many elif keywords can show up in an if-structure.
Conditional Expressions Involving Other Data Types
| Conditional Operator | Description |
| == | Tests if two numbers are equal. (Not the assignment operator) |
| != | Tests if two numbers are not equal. |
| > | Greater Than |
| < | Less Than |
| >= | Greater Than OR Equal |
| <= | Less Than OR Equal |
The common ways of testing conditions involving mathematical variables are given in the table above. Although inequalities such as > and < are on a standard keyboard, other inequalities, such as greater-than-or-equals and not-equals do not have a single keyboard button, so combinations of keyboard keys are used. Also note that when we test for equality in Python, two equal signs, ==, are used. A single equal sign is used to assign a value to a variable, not test it. Testing for equality also works for strings.
Code
if name == "Mary": @
~answer = "The person is Mary." @
elif name == "Jack": @
~answer = "The person is Jack." @
elif name == "Fred": @
~answer = "The person is Fred." @
elif name == "Paul": @
~answer = "The person is Paul." @
else: @
~answer = "I don't know who this person is."
What if name = "Paul"?
What if name = "Lidia"?
Note the difference between = and ==. Try not to get assignment and testing for equality mixed up.
Functions Containing If-Structures
It is possible to create functions that contain if-structures. The result is a more complex structure because this involves creating blocks of code that are contained in other blocks.
Absolute Value
def f(x): @
~if x >= 0: @
~~return -2*x @
~else: @
~~return 3*x
The above function uses different formulas depending on the number entered as an argument: f(1) == -2*1 == -2, while f(-1) == -3*(-1) == 3. More importantly for understanding Python code, notice that line 3 is a one line block with a header at line 2. However, lines 2, 3, 4, and 5 form a block with header at line 1. So line 3 is contained in two blocks, one for the if-statement and one for the function body. That is why it is indented twice. Generally, there is no limit to how many block levels there can be.
Section 1.5 Name:____________________
If-Statements
Score: /5
Problems
- Vocabulary Matching: Match each term with the best fitting description.
| if | _____ Checks if a condition is true after other condition(s) have been determined to be false. |
| else | _____ Comes before a block (section) of code that will execute if all other conditions in an if-structure are false. |
| elif | _____ Checks if an initial condition is true. |
- The following code involves an unusual grading scale. What will the grades be given the following scores?
Code
if score < 3: @
~grade = "F" @
elif score < 7: @
~grade = "D" @
elif score < 11: @
~grade = "C" @
elif score < 16: @
~grade = "B" @
else: @
~grade = "A"
| Score | Grade |
9 | |
| -2 | |
| 1 | |
| 16 | |
| 21 | |
| 7 | |
- Will the following be True or False?
| Expression | Value |
4 >= 7 | |
| 19 == 12 | |
| "Fred" == "Fred" | |
| "Fred" != "fred" | |
| 80 >= 80 | |
- Write code for an if-structure that takes a score variable, and assigns a letter grade to a variable called grade with the following scale: A: 80-100, B: 60-79, C: 40-59, D: 20-39, F: 0-19.
@@@@@@@@@@@@@@@@@@@@@@@@
Section 1.6: While Loops
Introduction
The keyword while is similar to if. Like if, while will execute a block of code if a condition is true. Unlike if, while will continue to execute code while the condition is true. A structure created by the while keyword is typically called a while-loop. A while-loop continues to loop around and execute code while the condition is true. An iteration is a single time through the loop.
Simple Counting While-Loop.
Code
counter = 0 @
while counter < 8: @
~counter += 1
The above while-loop will execute for 8 iterations of the loop. The variable counter is first set equal to 0, but then in line 3 inside the while-loop, 1 is added to make counter equal to 1. The next time through the loop, 1 is added to counter again. After this iteration counter is equal to 2. The loop continues to add 1 until counter is equal to 8. Notice when this happens the condition counter < 8 is now false and the loop stops. While the loop was executing, counter was equal to the numbers: 0, 1, 2, 3, 4, 5, 6, 7 one after the other until finally counter was equal to 8 and the loop came to an end. Variables that count, such as counter are very important when programming computers. They allow us to program our applications to do something a fixed number of times. Variables that count are frequently called iterators.
All Even Numbers from
1000 to
2000.
Code
it = 1000 @
while it <= 2000: @
~iter += 2
In the above while-loop the variable it (short for iterator) is equal to all of the even numbers from 1000 to 2000, one after another: 1000, 1002, 1004, 1006, ..., 2000. If for some reason we needed odd numbers instead we could have started with an odd number. If we needed multiples of 3 we could have added 3 each time.
It is important to note as well that, although it would take a person a long time to list out all 501 of these even numbers, a modern computer can generate these numbers with the above while-loop in microseconds. It is hard to fathom how fast modern computers really are.
Triangle Numbers.
Code
n = 10 @
it = 1 @
tri = 0 @
while it <= n: @
~tri += it @
~it += 1
In this example, a while-loop is used to calculate the 10th triangle number. Triangle numbers are calculated by adding all of the integers between 1 and a chosen integer. For example, the 3rd triangle number is 1+2+3 = 6, the 4th is 1+2+3+4 = 10. After the loop above is done executing the variable tri is equal to 1+2+3+4+5+6+7+8+9+10 = 55. The code above can be easily adjusted to calculate any triangle number just by changing the value of n.

Triangle Number Function
Code
def triangle_number(n): @
~it = 1 @
~tri = 0 @
~while it <= n: @
~~tri += it @
~~it += 1 @
~return(tri)
Above is a function containing the code from the previous example. This is also an example of placing a block within a block.
The Dangers of Infinite Loops
One pitfall of a while-loop is that it is very easy to create what is called an infinite loop. The condition of an infinite loop stays true forever, so the loop is stuck executing forever. This is one of the primary reasons programs sometimes freeze or crash. Poorly written code or unusual circumstances can cause a program to get stuck in an infinite loop. Typically a person or operating system is forced to kill the program. In more serious situations the entire operating system will crash and the computer must be restarted.
Simple Infinite Loop
Code
it = 1 @
while it > 0: @
~it += 1
In the above example, the variable it starts at 1 and only increases in the loop, never decreases. Therefore it will always be greater than 0. Notice then, the condition it > 0 must always be true. Any application with these lines of code will get stuck forever, or at least until someone or the operating system terminates the application.
Accidental Infinite Loop
Code
n = 10 @
it = 1 @
tri = 0 @
while it <= n: @
~tri += it
This example is a slightly altered version of the triangle number example. The only difference is that this example is missing the line of code it += 1 inside of the loop. This code will also create an infinite loop because it is never changed after it is initially set equal to 1. The condition is always true because it always stays less than n.
The break Keyword
There is an alternative way to stop a loop that does not depend on the condition. The break keyword puts on the breaks - it immediately stops a loop as soon as it is encountered. The break keyword is just briefly discussed here, but we will see later how it can be used to make code much more efficient.
Loop with a break Keyword.
it = 0 @
while it < 2000: @
~it += 1 @
~if it == 4: @
~~break
In the above code it may appear that the loop will execute until it reaches 2000. However, once it reaches 4, the condition of the if-statement inside the loop at line 4 is true. When this happens the break keyword is executed and the loop ends with it equaling 4.
Section 1.6 Name:____________________
While Loops
Score: /5
Problems
- Vocabulary Matching:
| while | ____ A loop that executes forever (at least until the program is terminated externally). |
| loop | ____ A Python keyword for writing code that repeatedly does something. |
| iteration | ____ Code the does something possibly multiple times. |
| infinite loop | ____ A single time through a loop. |
- What will be the different values of it be? How many iterations will the loop run?
it = 3 @
while it < 15: @
~it += 2
it = -10 @
while it < -2: @
~it += 1
it = 10 @
while it > 0: @
~it -= 1
it = 20 @
while it > 10: @
~it -= 3
- What will be the different values of it be? How many iterations will the loop run?
it = 0 @
while it < 100: @
~it += 1 @
~if it == 8: @
~~break
it = 6 @
while it < 100: @
~it += 2 @
~if it == 13: @
~~break
- What will be the different values of it be? Hint: Don't actually try to write them all out. How many iterations will the loop run?
it = 0 @
while it < 100000000: @
~it += 10
- Write code to create a loop that will iterate through all of the even numbers between 100 and 500. So 100, 102, 104, 106, ... 496, 498, 500.
@@@@@@@@@@

